ピタゴラスの定理
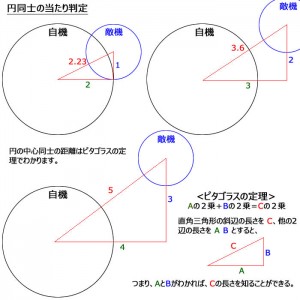
ゲームの当たり判定を実装するときに、円の中心同士の距離は、ピタゴラスの定理でわかります。
自機の中心から敵機の中心までの距離が、自機と敵機の半径を足したものより小さければ当たっている計算になります。
自機の半径を2、敵機の半径を1とします。
ピタゴラスの定理で、斜辺が約2.23のとき、つまり自機と敵機の距離が2.23のとき、自機の半径+敵機の半径(2+1=3)と比べて、斜辺の方が小さいので当たっている。
ピタゴラスの定理で、斜辺が5のとき、つまり自機と敵機の距離が5のとき、自機の半径+敵機の半径(2+1=3)と比べて、斜辺の方が大きいので当たってない。