比較演算
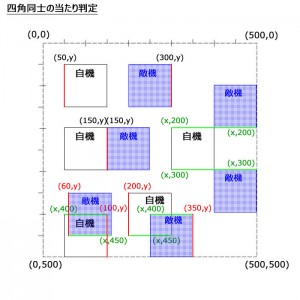
前回、円同士の当たり判定を考えてみましたが、当たりの範囲を四角にした場合は、どうなるでしょう。
当たっている時の条件は、
自機の左側のx座標より、敵機の右側のx座標が大きい、かつ、
自機の上側のy座標より、敵機の下側のx座標が大きい、かつ、
自機の右側のx座標より、敵機の左側のx座標が小さい、かつ、
自機の下側のy座標より、敵機の上側のx座標が小さい。
ややこしいですね、例えば
自機の左側のx座標(50)より、敵機の右側のx座標(300)が大きい、正
自機の上側のy座標(50)より、敵機の下側のx座標(150)が大きい、正
自機の右側のx座標(150)より、敵機の左側のx座標(200)が小さい、違うー!
自機の下側のy座標(150)より、敵機の上側のx座標(50)が小さい。正
当たってない。
例えば
自機の左側のx座標(50)より、敵機の右側のx座標(160)が大きい、正
自機の右側のx座標(100)より、敵機の左側のx座標(60)が小さい、正
自機の上側のy座標(400)より、敵機の下側のx座標(450)が大きい、正
自機の下側のy座標(500)より、敵機の上側のx座標(350)が小さい。正
当たってる。
例えば
自機の左側のx座標(200)より、敵機の右側のx座標(350)が大きい、正
自機の右側のx座標(300)より、敵機の左側のx座標(250)が小さい、正
自機の上側のy座標(350)より、敵機の下側のx座標(500)が大きい、正
自機の下側のy座標(450)より、敵機の上側のx座標(400)が小さい。正
当たってる。